Uncertainty in measurement

Measurement uncertainty

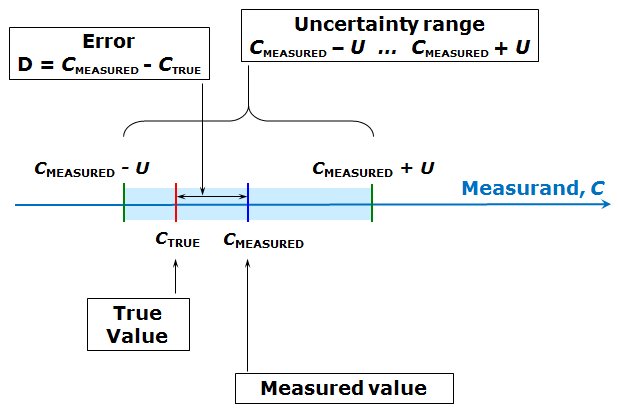
Measurement uncertainty is defined as a “parameter, associated with the result of a measurement, that characterizes the dispersion of the values that could reasonably be attributed to the measurand” (JCGM).
Measurement uncertainty is a parameter used in data processing for the description of both the dispersion of the result and its estimated difference from the accurate value. Frequently, this is simplified to only dispersion, and measurement uncertainty is obtained using statistical data variance. As a basic source for uncertainty processing, we refer to the Guide to the Expression of Uncertainty in Measurement (GUM) available from Bureau International des Poids et Mesures (BIPM). The basic idea behind it is to express mathematically the measurement, get all the uncertainties of input quantities, including both the statistical and systematic effects, and to calculate an uncertainty of the measurement results.

Uncertainty components

Measurement uncertainty is usually divided in two components:
Type A uncertainty expresses the random error in the data, typically caused by noise and similar environmental conditions. Its evaluation is based on statistical tools.

Type B uncertainty describes a systematic error that could be present in the result, and we do not know it to a level that we could correct it. This uncertainty is usually evaluated using Gauss law for propagation of uncertainties. We first construct a mathematical model of the measurement—an equation describing the measurement process including the systematic error sources. Measurement errors are impossible to avoid, although we can minimize their magnitude by good measurement system design accompanied by appropriate analysis and processing of measurement data. Random errors which are also called precision errors in some books are perturbations of the measurement either side of the true value caused by random and unpredictable effects, such that positive errors and negative errors occur in approximately equal numbers for a series of measurements made of the same quantity. Disturbance of the measured system by the act of measurement is a common source of systematic error.